Posted by: M P 16 years, 8 months ago
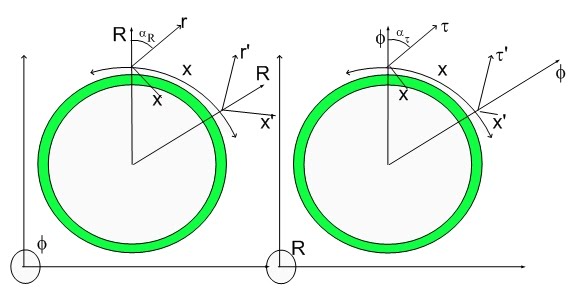
The Origin of v/c ratio
In the Hypergeometrical Universe model, the expansion of the 3D Universe Hypersphere happens at the speed of light (c).
Motion within our 3D Universe is seem to be transversal to the radial direction of propagation. This means that v/c is the tangent of the angle of propagation.

This is the reason v/c exists in Relativity and in my theory. In fact, in Relavity the beta factor is just part of Lorentz transformation which later was reinterpreted by Einstein as a metric of the physical space..:)
In explaining the Precession of Mercury Perihelion I was able to refer to the work of Gerber who in 1898 used the same potential my theory derives. In fact, I didn't find the original work from Gerber in the internet but a work by Jaume Gine.
The equation for the Hypergeometrical Gravitational potential.

Gine tried to rederive Gerber's work starting from a retarded potential paradigm. The problem with that is that is generates higher order derivatives. He failed to understand the geometric origin of that term which can only be understood in a 4D spatial manifold paradigm. All velocity ratios in my theory are due to angles either with respect to the fourth spatial dimension R or within the 3D hypersphere (as in the Biot-Savart law derivation).
In the case of moving dilators ratio between velocities are still angles and do not require higher order derivatives for their definition.
Please feel free to read the derivation of Gyrogravitation and Magnetism (Biot-Savart Law) . I've just take a different angle on the subject..:)
Cheers,
MP
Archive
2017
2016
2015
2014
2013
2012
2011
2010
2009
2008
- December (5)
- November (4)
- October (13)
- September (7)
- August (5)
- July (6)
- June (5)
- May (5)
- April (7)
- March (6)
- February (7)
- January (5)
2007
- December (4)
- November (13)
- October (10)
- September (3)
- August (24)
- July (12)
- June (2)
- May (1)
- March (4)
- February (12)
- January (4)
2006
Categories
- Brian Greene (1)
- Censorship (8)
- Coherent Nuclear Fusion (1)
- Erik Anson (3)
- Hypergeometrical Universe (290)
- Kip Thorne (1)
- Lawrence M. Krauss (1)
- Max Tegmark (1)
- Michio Kaku (2)
- Neil deGrasse Tyson (1)
- Paul Ginsparg (1)
- Science News (2)
- Sheldon Glashow (1)
- The Undiscovered Continent (1)
Comments
There are currently no comments
New Comment